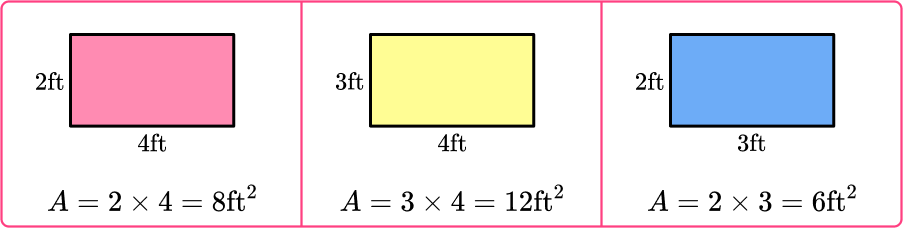What is the Surface Area of a Square? - Unlocking the Secrets of Geometry

To find the surface area of a square, we need to calculate the area of all its sides. Since a square has four equal sides, the formula for the total surface area can be calculated as:

Surface Area = 4 x side length x side length

• Measure the length of one side of the square.
• Multiply the side length by itself to get the area of one side.
• Since all sides of a square are equal, multiply the area of one side by 4 to get the total surface area.

For example, if the side length of a square is 5 units:

Surface Area = 4 x 5 x 5 = 4 x 25 = 100 square units

Therefore, the surface area of a square with a side length of 5 units would be 100 square units.

The surface area of a square is a measure of the total space enclosed by the square\"s four sides. It represents the amount of two-dimensional space covered by the square. Understanding this concept is crucial in both basic geometry and real-life applications, as it helps in calculating the material needed for construction, crafting, and more.

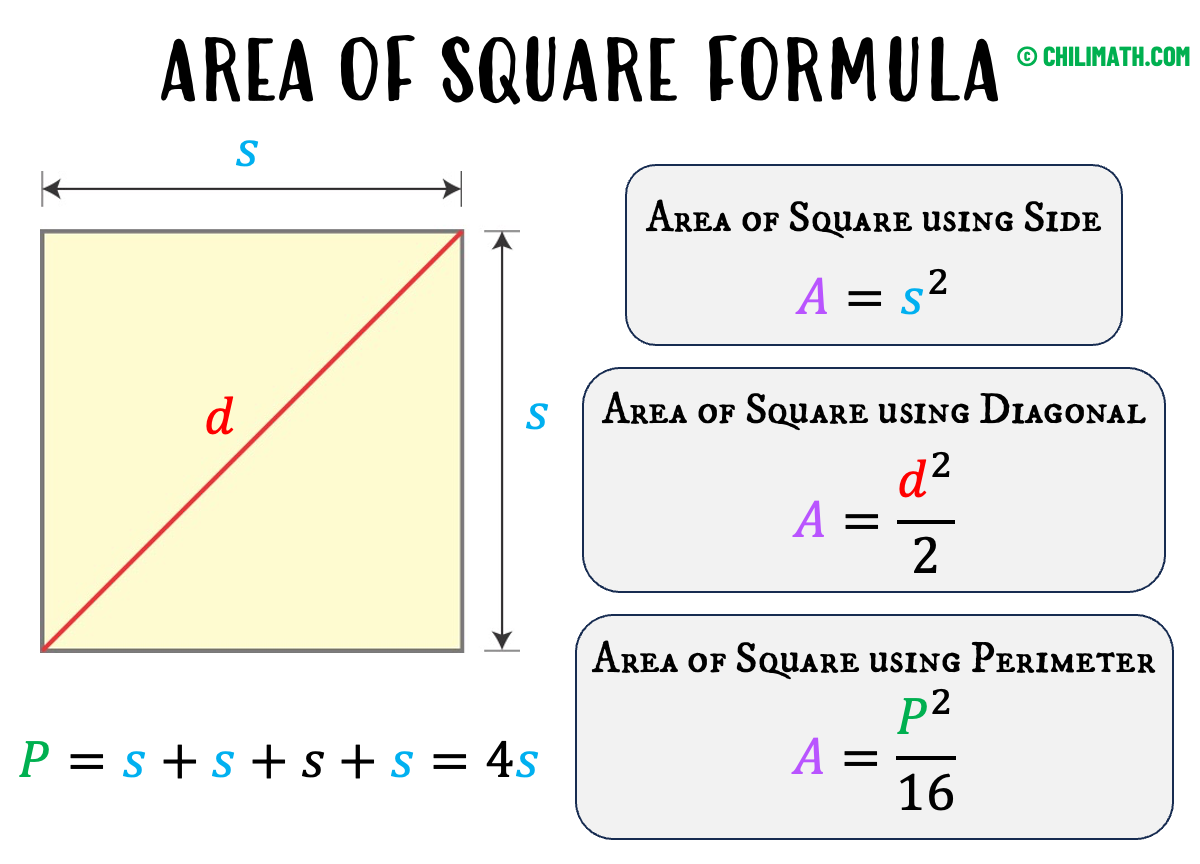
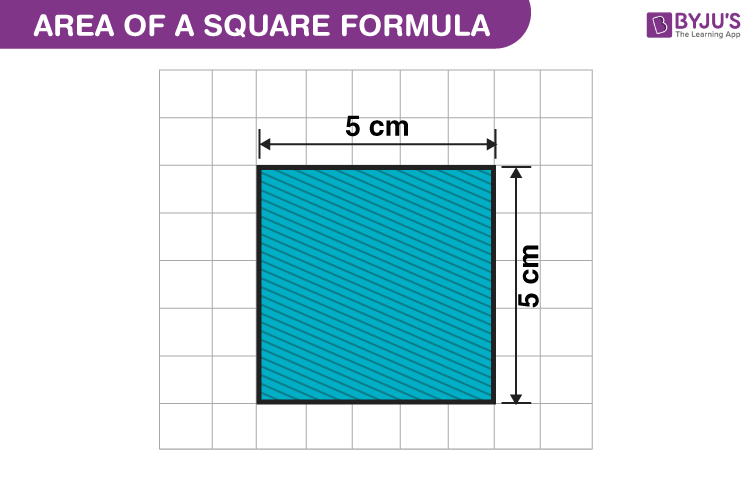
To calculate the surface area of a square, you use the formula A = s^2, where A is the area and s is the length of one side of the square. This formula implies that you square the length of the side to find the square\"s surface area.

1. Identify the length of one side: Measure or find out the length of one side of the square (s).
2. Apply the formula: Use the formula A = s^2 to calculate the surface area.
3. Interpret the result: The resulting value is the total area covered by the square\"s surface in square units.

This basic concept serves as the foundation for more complex geometric calculations and is essential for students and professionals working with spatial designs.

The surface area of a square, which is a measure of the total area that the surface of the square covers, can be calculated using a simple formula. This formula is essential for understanding how to determine the amount of space a square occupies on a flat surface.

The formula for calculating the surface area of a square is:

Surface Area = side × side

or simply,

Surface Area = s²

where s represents the length of one side of the square. Since all sides of a square are equal in length, you only need to know the length of one side to calculate its surface area.

This formula is derived from the basic principle that a square has four equal sides, and the area is calculated by multiplying the length of one side by itself. It is a specific case of the formula for the area of a rectangle (length × width), where the length and width are the same for a square.

Here\"s a step-by-step guide on how to use the formula:

1. Measure the length of one side of the square (s).
2. Plug the measurement into the formula by multiplying the side length by itself (s × s or s²).
3. The result will give you the surface area of the square in square units (for example, square meters, square feet, etc.).

It\"s important to ensure that the unit of measurement for the side length is squared in the final answer, as the area is always expressed in square units.

To calculate the surface area of a square accurately, follow these simple steps. This guide assumes you already know the length of one side of the square, which is all you need thanks to the square\"s all sides equal property.

1. Identify the Length of One Side: Begin by measuring or obtaining the length of one side of the square. Since all sides of a square are equal, you only need the length of one side.
2. Use the Formula: Recall the formula for calculating the surface area of a square is Area = side × side or Area = side^2, where side is the length of the square\"s side.
3. Substitute the Value: Substitute the length of the side into the formula. For example, if one side of the square is 4 units, the calculation would be Area = 4 × 4 or Area = 16 square units.
4. Calculate: Perform the multiplication to find the area. This is the total surface area the square covers.
5. Result: The result from the calculation gives you the surface area of the square in square units. This number represents the total area covered by the square.

This step-by-step guide simplifies the process of calculating the surface area of a square, making it accessible for educational purposes, DIY projects, and more. Remember, the key to accurate calculation is ensuring the measurement of the side is precise.

Understanding the formula for calculating the surface area of a square is essential, but seeing examples can help clarify the process. Here are a few scenarios to demonstrate how to apply the formula in practical situations.

1. Example 1: A square with a side length of 4 meters.
2. To find the surface area, you would use the formula Area = side × side. So, for a square with a side length of 4 meters, the calculation would be Area = 4m × 4m = 16 square meters.
3. Example 2: A square plot of land with each side measuring 10 meters.
4. Using the same formula, the surface area is calculated as Area = 10m × 10m = 100 square meters. This example illustrates the surface area of a piece of land that could be used for gardening or construction.
5. Example 3: A square tile with a side length of 0.5 meters.
6. In this case, the surface area would be Area = 0.5m × 0.5m = 0.25 square meters. This calculation can help in determining how many tiles are needed to cover a certain area of a floor or wall.

These examples demonstrate the versatility of the formula for calculating the surface area of a square and how it can be applied in various real-world situations, from construction projects to interior design.

Understanding the surface area of a square has practical applications in various aspects of everyday life and professional fields. From architecture to crafting, the ability to calculate the surface area of a square enables precise planning, efficient use of materials, and optimization of space. Here are some common applications:

• Architecture and Construction: Calculating the surface area of square-shaped materials or spaces is crucial for determining the amount of paint, flooring, or other materials needed for construction and renovation projects.
• Landscaping: Knowing the surface area of square plots of land helps in planning garden layouts, irrigation systems, and outdoor constructions, ensuring that resources are used efficiently.
• Interior Design: Designers use surface area calculations to select the right sizes of rugs, tiles, and wall coverings, ensuring that the dimensions fit perfectly within square spaces.
• Educational Projects: Teachers often incorporate surface area calculations into math and science projects, helping students understand geometric concepts and their real-world applications.
• Crafting and DIY Projects: For those engaged in crafting, sewing, or woodworking, calculating the surface area of square pieces is essential for ensuring that materials are cut and utilized without wastage.
• Manufacturing: In manufacturing, especially in industries like packaging, knowing the surface area is important for designing products that meet specific size and material requirements.

These examples highlight the importance of understanding how to calculate and apply the concept of square surface area in various scenarios, emphasizing its relevance beyond academic exercises.

When calculating the surface area of a square, there are several common mistakes that can lead to incorrect results. Being aware of these pitfalls can help ensure accurate calculations.

1. Not Using the Correct Formula: Confusing the formula for the surface area of a square with that of other shapes, like rectangles or triangles, can lead to errors. Remember, the formula for a square\"s surface area is side × side.
2. Incorrect Measurement Units: Failing to use consistent measurement units throughout the calculation can result in errors. Ensure all measurements are in the same units (e.g., all in meters or all in feet).
3. Misinterpreting the Side Length: Sometimes, the length of one side is given, and it\"s mistakenly assumed to be the length of all sides. In a square, all sides are equal, so this should not be an issue, but double-checking is always beneficial.
4. Calculation Errors: Simple arithmetic mistakes can lead to incorrect surface area calculations. Double-check your work for accuracy.
5. Overlooking the Power of Squaring: The formula involves squaring the side length. Ensure you are actually squaring the side length rather than just multiplying it by 2.

By being mindful of these common errors, you can improve the accuracy of your surface area calculations for squares and avoid potential mistakes.

Calculating the surface area of a square can be greatly simplified with the use of various tools and calculators. These resources can help both students and professionals to accurately compute surface areas without the need for manual calculations, saving time and reducing the potential for errors.

• Online Surface Area Calculators: Numerous websites offer free calculators specifically designed for computing the surface area of squares. These tools typically require you to enter the length of one side of the square, and they automatically calculate the area for you.
• Math Software: Software programs like Mathematica, MATLAB, and GeoGebra provide functions to calculate surface areas. These tools are beneficial for more complex calculations and for visualizing the geometry of shapes.
• Mobile Apps: There are many mobile applications available for both Android and iOS devices that offer quick and easy surface area calculations. These apps are particularly useful for on-the-go calculations and for educational purposes.
• Spreadsheet Programs: Excel and Google Sheets can be used to create formulas that calculate the surface area of squares. This is especially useful for handling multiple calculations at once and for integrating this data into larger projects.

Utilizing these tools and calculators can significantly ease the process of computing the surface area of squares. Whether for academic, professional, or personal projects, these resources ensure accurate and efficient calculations.

• What is the formula for calculating the surface area of a square?
• The formula to calculate the surface area of a square is A = s^2, where A is the area and s represents the length of one side of the square.
• Can the surface area of a square be negative?
• No, the surface area of a square cannot be negative because it represents a physical space which cannot have a negative measurement.
• How do you find the surface area of a square when given the diagonal?
• To find the surface area from the diagonal, use the formula A = (d^2) / 2, where d is the length of the diagonal. This formula comes from the relationship between the diagonal and the sides of a square in a right triangle.
• Is the formula for the surface area of a square the same as for a cube?
• No, the formula for the surface area of a square is different from that of a cube. For a square, it\"s A = s^2. For a cube, it\"s A = 6s^2, where s is the length of one edge of the cube.
• Why is it important to know the surface area of a square?
• Knowing the surface area is important for various practical applications, such as tiling a floor, wrapping a gift, or allocating space for construction projects.
• Can I use the surface area formula for rectangles too?
• No, the formula A = s^2 is specific to squares. For rectangles, you should use the formula A = length × width, as their sides can have different lengths.

Understanding the surface area of a square unlocks a world of practical and theoretical applications. Whether for academic pursuits, professional projects, or everyday problems, mastering this concept can provide valuable insights and solutions.